2-00. Algorithmes gloutons

En informatique, on rencontre souvent des problèmes d’optimisation, c’est-à-dire des problèmes pour lesquels on cherche la meilleure solution possible satisfaisant un certain nombre de contraintes parmi un grand nombre de solutions.

Les problèmes d’optimisation

Les problèmes d’optimisation sont des problèmes possédant un très grand nombres de solutions pour lesquels on recherche la meilleure solution possible.

Il faut donc avoir un critère pour évaluer la qualité d’une solution.

En voici quelques exemples :

Problème du voyage de commerce : un représentant de commerce doit trouver un itinéraire passant par plusieurs villes données et revenir à son point de départ. L’optimisation recherchée est de rendre se trajet le plus court possible.
Problème du rendu de monnaie : un commerçant doit rendre la monnaie en fonction des pièces dont il dispose. L’optimisation recherchée est de rendre minimum le nombre de pièces rendues.
Problème de l’optimisation de créneaux horaires : un établissement dispose d’un certain nombre de salles dans lesquelles doivent se dérouler des événements de durée variable. L’optimisation recherchée est d’avoir le maximum d’événements possibles.

Problème du voyageur de commerce

Un voyage de commerce part d’une ville A, doit passer par les villes B, C, D et E, puis revient en A. L’ordre de villes visités doit être tel que la distance qu’il doit parcourir en partant de A pour revenir en A doit être minimale.

graphe représentant les villes et les distances — Villes à visiter et distance séparant ces villes

On peut calculer qu’il y a 4×3×2×1 = 24 parcours possibles. Comme le sens du parcours n’a pas d’importance, vu qu’il ne changera pas la distance parcourue, ça fait 12 parcours à considérer.

Vu que ça n’en fait pas beaucoup, on peut s’amuser à les considérer tous.

Itinéraire	Somme	Total
ABCDEA ou AEDCBA	130+90+30+80+100	430
ABCEDA ou ADECBA	130+90+50+80+170	520
ABDCEA ou AECDBA	130+60+30+50+100	370
ABDECA ou ACEBDA	130+60+80+50+70	390
ABECDA ou ADCEBA	130+160+50+30+170	540
ABEDCA ou ACDEBA	130+160+80+30+70	470
ACBDEA ou AEDBCA	70+90+60+80+100	400
ACBEDA ou ADEBCA	70+90+160+80+170	570
ACEBDA ou ADBECA	70+50+160+60+170	510
ACDBEA ou AEBDCA	70+30+60+160+100	420
ADBCEA ou AEDBDA	170+60+90+50+100	470
AEBCDA ou ADCBEA	100+160+90+30+170	550

On voit que le circuit optimal, c’est-à-dire le plus cours, fait 370 km. Le problème est que la quantité de possibilités croît exponentiellement. Si on a 10 villes à considérer, il y a 9!÷2 = 181.400 circuits possibles. La complexité du problème est donc en O(n!), ce qui devient vite ingérable.

Lorsqu’on calcule toutes les possibilités, on voit bien qu’on envisage des possibilités absolument pas intuitives, comme par exemple ADBCEA. Une machine n’ayant pas (encore ?) d’intuition, il faut essayer de trouver un algorithme qui s’en approche. Et il s’agit de l’algorithme glouton (greedy en anglais).

Principe d’un algorithme glouton

Résoudre un problème grâce à un algorithme glouton.

Le principe de l’algorithme glouton (greedy algorithm en anglais) est simple : choisir la meilleure option, au point où on se trouve, sans se soucier des conséquences.

Une personne avide (traduction plus fidèle de greedy) – généralement de pouvoir ou d’argent, va chercher à augmenter sa fortune ou son pouvoir dans l’immédiat sans se préoccuper des conséquences. Elles appliquent littéralement un algo glouton à leur recherche.

Je vous mets au défi de trouver, dans les 100 plus grandes fortunes mondiales, un individu se souciant dans conséquences éthiques, sociales ou environnementales de sa stratégie d’enrichissement.

Le fait que ce comportement soit parfois considéré avec admiration alors qu’il est souvent criminel laisse d’ailleurs songeur.

Si on applique cet algorithme au problème du paragraphe précédent, voici ce qu’on obtient.

Le voyageur va d’abord alors en C, qui est la ville la plus proche de A, puis il ira en D, puis en B, puis en E et reviendra en A.

On obtient donc le trajet ACDBEA, qui fait 420 km. Ce n’est pas le meilleur (un algo glouton ne permet pas toujours d’obtenir la meilleure solution), mais c’est une solution raisonnablement bonne. Et surtout, c’est une solution de complexité O(n), et non pas O(n!).

Un algorithme glouton cherche à optimiser localement chaque étape d’un problème, plutôt que le problème dans son ensemble.

Cela ne garantit pas que la solution trouvée soit la meilleure, mais il fournit généralement une solution plutôt bonne.

Sa complexité est très nettement inférieure à une approche « naïve » consistant à déterminer toutes les solutions possibles avant de choisir la meilleure.

Exemples d’application

Problème du rendu de monnaie

1. Compléter la fonction ci-dessous qui prend en argument un montant et une liste de pièces/billet et qui renvoie la liste minimale de billets et de pièces pour attendre ce montant.


			def rendu_glouton(montant, systeme):
				rendu = []
				for p in ...:
					while ...:
						rendu ...
						montant ...
				return rendu

2. Tester la fonction pour un montant de 63 € et un montant 0,63 €, avec le système [50, 20, 10, 5, 2, 1, 0.5, 0.2, 0.1, 0.05, 0.02, 0.01]. Commenter

3. Proposer une solution au problème soulevé à la question précédente

4. Tester la fonction pour un montant de 63 € sachant qu’on ne dispose ni de billets de 5 €, ni de billets de 10 € [50, 20, 10, 5, 2, 1, 0.5, 0.2, 0.1, 0.05, 0.02, 0.01]. La solution obtenue est-elle optimale ?

Correction

1. Fonction rendu_glouton


				def rendu_glouton(montant, systeme):
					rendu = []
					for p in systeme:
						while p <= montant:
							rendu.append(p)
							montant -= p
					return rendu

2. L’algo ne marche pas bien pour la somme 0.63. Ceci est dû à la manipulation de float.

3. On peut éviter ce problème en travaillant avec des centimes.

4. Le rendu obtenu est [50, 2, 2, 2, 2, 2, 2, 1]. La solution optimale serait [20, 20, 20, 2, 1]

Maximisation d’une somme sous contrainte

On cherche à sélectionner cinq nombres de la liste suivante en cherchant à avoir leur somme la plus grande possible et en s’interdisant de choisir deux nombres voisins.

15 4 20 17 11 8 11 16 7 14 2 7 5 17 19 18 4 5 13 8

Pour répondre à cette question, on va utiliser un algorithme glouton dont la règle de choix est la suivante :

À chacune des cinq étapes, choisir le plus grand nombre possible dans les choix restants.

1. Sur quelle idée simple est basée cette règle de choix ?

2. On donne ci-dessous les deux premières étapes de l’algorithme glouton. Compléter les étapes restantes.

on choisit le 20 et on raye ses deux voisins 4 et 17 à cause de la contrainte.
on choisit le 19 et on raye ses deux voisins 17 et 18 à cause de la contrainte.
…
…
…

Quel résultat fournit cet algorithme ?

3. Sur cet exemple, est-ce que l’algorithme glouton est effciace ?

Minimisation d’une somme

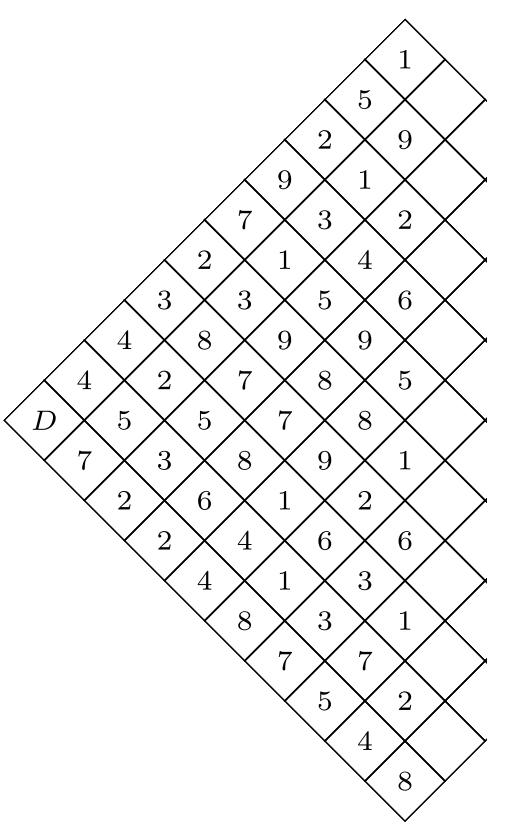
Sur la grille ci-contre/ci-dessus, on part de la case à gauche marquée de la lettre D et on souhaite atteindre une des cases vides sur la partie droite en se déplaçant de case en case.
Lorsqu’on est sur une case on peut se déplacer sur une des deux cases voisines situées sur la droite. On note S la somme de toutes les cases traversées.

Par exemple on peut effectuer la trajectoire D → 7 → 5 → 3 → 5 → 7 → 9 → 8 → 9 → 6 qui conduit à S = 59.

On cherche à effectuer la trajectoire qui rend la somme S la plus petite possible.

1. Que cherche-t-on à sélectionner ? Quelles sont les contraintes ? Quelle est l’optimisation recherchée ?

2. Déterminer une règle de choix qui permet de définir un algorithme glouton. Quelle trajectoire et quelle somme S obtenez-vous sur cet exemple avec votre algorithme glouton ?

3. Sur cette grille, la trajectoire optimale donne une somme S = 23. Votre algorithme glouton a-t-il trouvé une solution acceptable ?

4. Pour obtenir la solution optimale de façon certaine, on souhaite trouver toutes les trajectoires possibles et calculer pour chacune d’elles la somme associée. Justifier qu’on va trouver 512 trajectoires.